塾長ブログ

先日紹介した『算数オリンピック』。
世界中の子供たちが算数への関心を高め、お互いに共感し、子供たちの独創性と思考力を育てる目的で毎年開催されています。

『算数オリンピック』のサイトはこちら

そしてその中の問題を一つ出してみましたが、皆さん解けましたでしょうか。
小学生の問題ですが、意外と難しかったのではないでしょうか。
固定概念に縛られず、柔軟な発想とひらめきが求められます。

本日はその解答をお教えします。

先ずは問題の確認です。

［問題］
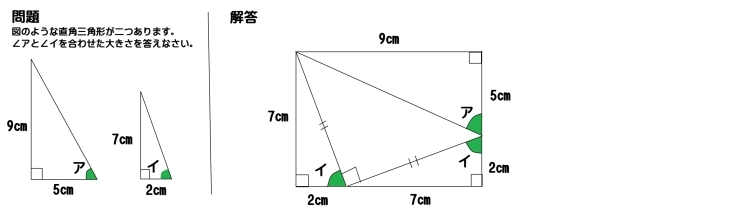
問題の図を見てください。
上の図のような直角三角形が二つあります。
三角形の直角を挟む辺の長さは一つが9㎝と5㎝、もう一つが14㎝と4㎝です。
では、角のアとイを合わせた大きさは何度でしょうか。

では解答です。

［解答］
2種類の直角三角形があるのですが、そのうちの直角を挟む辺の長さが2㎝と7㎝の方をもう一つ用意します。
そして上の図のように並べると長方形ができます。
そうすると中央に直角二等辺三角形ができるのが分かりますか。
長方形の右側の辺を見ると、その直角二等辺三角形の直角でない角を挟んで、∠アと∠イが向かい合っているのが見えます。
当然直角二等辺三角形の直角でない角は45°なので∠アと∠イを足した大きさは180°から45°を引いた135°となります。

∠ア+∠イ＝180°-45°＝135°

どうでしょうか。
与えられた辺を見て、2㎝+5㎝＝7㎝、2㎝+7㎝＝9㎝で長方形が作れるという点に気づくかどうか、そして、三角形を組み合わせて作った長方形の中に直角二等辺三角形ができることに気づくかどうかが問題です。
聞けばなるほどという感じではありませんか。
このような問題が算数オリンピックではたくさん出ます。
学校の決まり切った問題しか解けないと難しいですね。

子供のころは頭が柔らかく、本当に柔軟な発想が生まれやすいのですが、学校の勉強が忙しく与えられた紋切り型の問題を解くので精一杯な教育では、この素質を台無しにしてしまいます。
時にはこのように「アッ、なるほど！」というような問題もやらせて、やわらか頭を育てると同時に勉強を楽しく、関心を高めてほしいと思います。

そして、このような基礎知識からひらめきや論理を通して解答を導く、というのが現在文科省が目指す教育なのです。
言うは易く行うは難し。
簡単に言ってくれますが、そう思うように発想が出ないですよね。
それを出せるようにする教育。
これから本格的に教育改革が実践され、どのような成果が出るのか注視する必要があります。